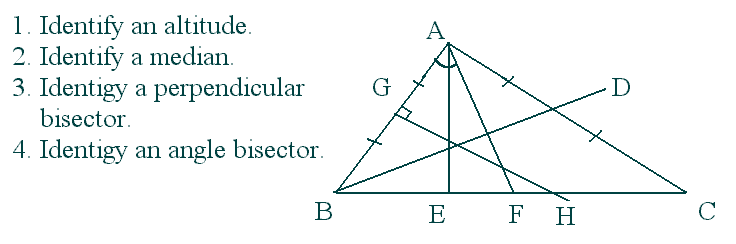Applying Congruent Triangles

Segments of a triangle:

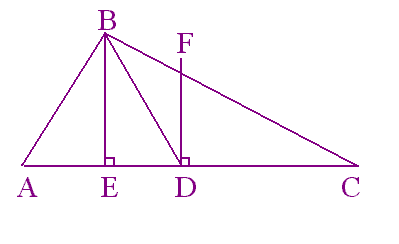
BD is a median - crosses AC at the midpoint.

BE is an altitude - perpendicular with AC

DF is perpendicular bisector - perpendicular to AC and crosses at the midpoint of AC also.

Angle Bisector - cuts an angle in half.
BD is an angle bisector if ÐABD equals  ÐDBC.

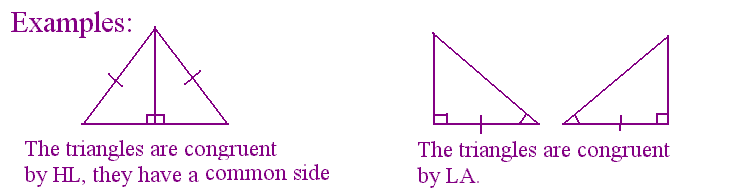
Congruence for right triangles:

LL the legs of two right triangles are congruent then the two triangles
            are congruent.
HAthe hypotenuse and an angle are congruent then the two triangles
            are congruent.
LA one  leg and one angle are congruent the the two triangles are
            congruent.
HL the hypotenuse and one leg are congruent then the two triangles
            are congruent.

The sum of any two sides of a triangle is greater than the third.
    Ex. A polygon with sides 5, 13, and 18 is not a triangle because
                The sum of 5 and 13 is not greater than 18, they equal 18.
    Ex. A polygon with sides 8, 14, and 25 is a triangle because
                The sum of 8 and 14 is greater than 25

EXAMPLE PROBLEMS