Surface Area and Volume

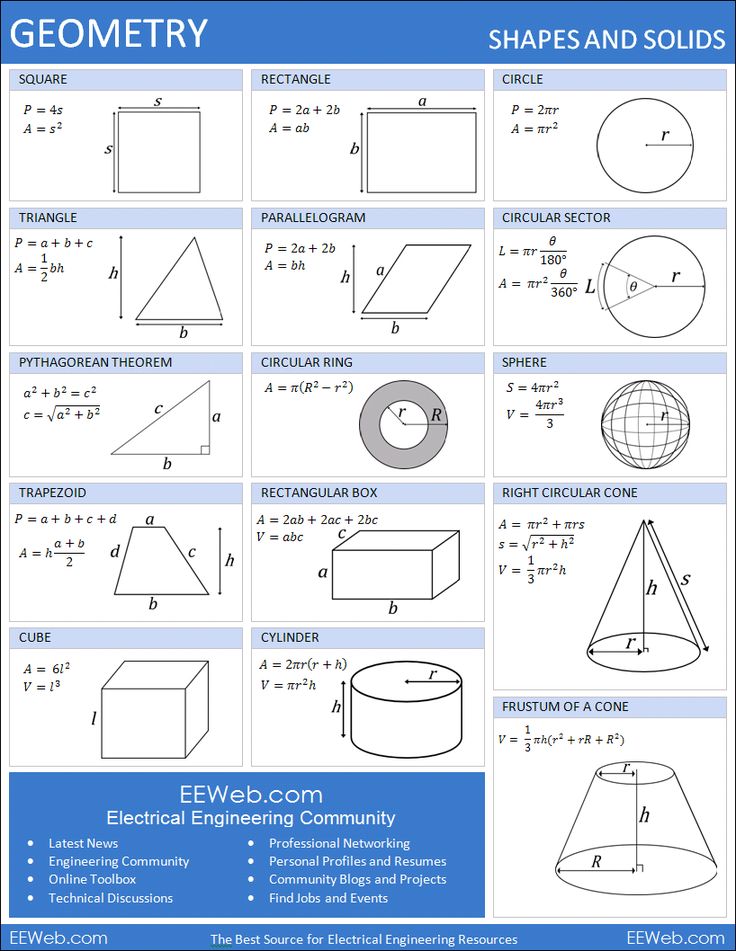
All formulas needed for area or volume in this chapter:

                     Examples:                              

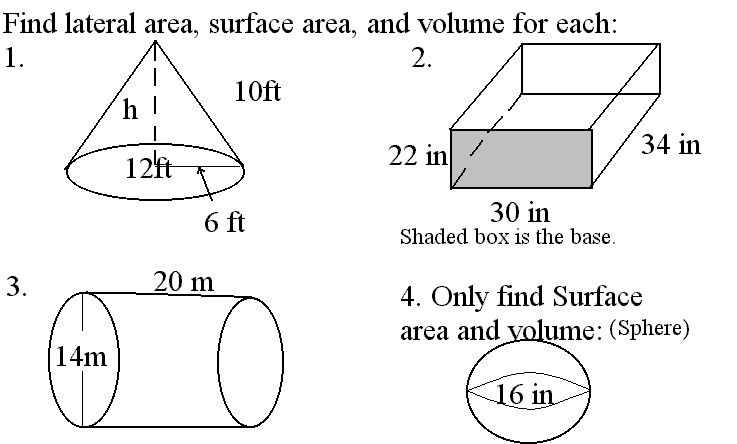
1. Find the lateral area, surface area, and volume of the   
    prism with an equilateral triangular base with sides 6in.
    Have to get area and perimeter of the triangular base:
    Have to use Pythagorean theorem to find the height of the triangular base.
      

h2 + 32 = 62     h = 5.2 m
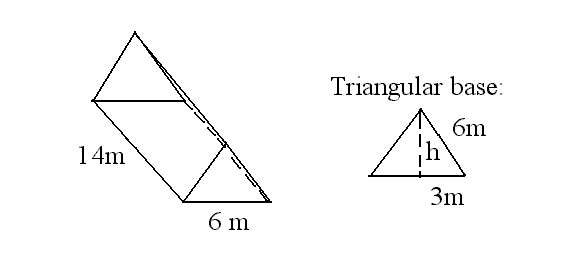
Area of the triangular base is (1/2)(5.2)(6)
Area = 15.6 m2
Perimeter of the triangular base is 6+6+6
Perimeter = 18 m
Lateral Area = Ph or (18)(14) = 252 m2
Total Surface Area = Ph+2B
(18)(14)+2(15.6) = 283.2 m2
Volume = Bh or
(15.6)(14) = 218.4 m3

                                                  
2. Find the lateral area, surface area, and volume of the cylinder
 

Lateral area = 2(3.14)(6.5)(20) = 816.4 in2

Surface area = 2(3.14)(6.5)(20) + 2(3.14)(6.52)
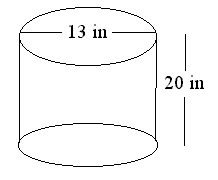
1081.73 in2

Volume = (3.14)(6.52)(20)
2653.3 in3

 

3. Find the lateral area, surface area, and volume of the
    pyramid.

 First find the height using Pythagorean Theorem,
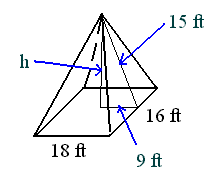
            h2 + 92 = 152             h = 12 ft
Find the perimeter and area of the rectangular base -   P = 2(18)+2(16) = 68 ft
       A = (18)(16) = 288 ft2
Lateral area = (1/2)Pl or (1/2)(68)(15) = 510 ft2
(l is slant height which is 15 ft)
Surface area = (1/2)Pl+B or
(1/2)(68)(15)+(288)= 798 ft2
Volume = (1/3)Bh or (1/3)(288)(12) = 1152 ft3

Example Problems