

Polygons and Area
A polygon is a figure with straight, connected sides.
Polygons:
| Number of sides | Polygon |
| 3 | triangle |
| 4 | quadrilateral |
| 5 | pentagon |
| 6 | hexagon |
| 7 | heptagon |
| 8 | octagon |
| 9 | nonagon |
| 10 | decagon |
| 12 | dodecagon |
| n | n-gon |
A regular polygon is a polygon with congruent sides and congruent angles.
Interior angle sum = 180(n-2) {n is number of sides}
Exterior angle sum = 360
The sum of the interior
and exterior angles measure 180 degrees.
EX: Find the exterior angle if the interior angle is 45.
180 - 45 = 135
To find the number
of sides, divide 360 by exterior angle.
(because exterior angle sum is always 360)
EX: Find the number of sides given the exterior angle is 45.
360/45 = 8 sides
EX 2: Find the exterior angle given there are 9 sides.
360/9 = 40 degrees
If you are given
one interior angle, subtract from 180 to get exterior angle, then divide 360
by exterior angle.
EX: Find the number of sides given the interior angle is 108.
180 - 108 = 72 then 360/72 = 5 sides
Only need Area Formulas from this formula sheet for this chapter:

Examples:
1. Find the area of the triangle
|
|
Find the base
first: |
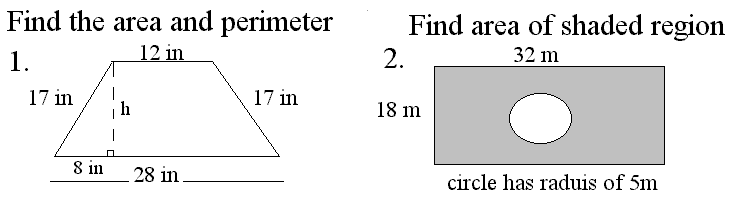
2. Find the perimeter and area
of the trapezoid
|
|
P = 10+8+8+16
= 42 in |
3. Find the area and
perimeter of the equilateral triangle base
with sides 6in.
Have to use Pythagorean theorem to find the height of the
triangle:
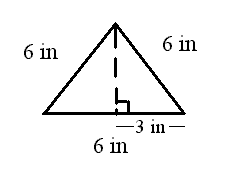 |
h2 + 32
= 62 |
Example Problems
3. Find the sum of the measure of the interior angles of a
pentagon.
4. How many sides does a polygon have if the exterior angle
measures 20?
5. Find the area of a rhombus with diagonals 15 in and 17 in.
6. Find the area of a circle with diameter of 16 ft.
7. Find the circumference of a circle with radius of 22 m.
8. Find the number of sides of a polygon if the interior angle
measures 165.
9. Find the area of a triangle with base 8 in and height 12 in.
10. Find the area of an equilateral triangle with sides 10 in.