Chapter 9

Analyzing Circles

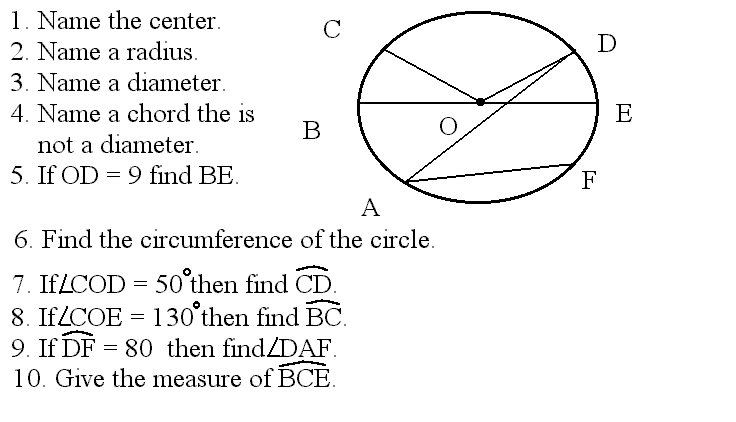
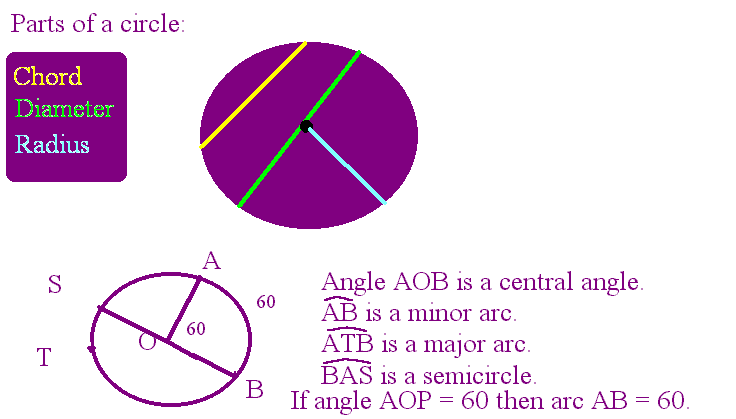
Circle is the set of all points in a plane that are a given distance from a given point called the center.

The radius is the segment from the center to a point on the circle.

A chord is the segment that has both endpoints on the circle.

A diameter is a chord that contains the center of the circle.

*The radius is half the diameter.*

Circumference of a circle is the distance around the circle.
Formula: C = 2&r

Central angle of a circle is an angle inside the circle with vertex on the circle. The central angle separates the circle into two arcs.

Minor arc is less than 180 degrees.
Major arc is greater than 180 degrees.
The measure of the minor arc is the measure of the central angle.

Semicircle is arc that equals 180 degrees.
(Half the circle.)
Inscribed polygon is a polygon with vertices lie on the circle.

If a diameter is perpendicular to a chord then it bisects the chord and the arc.

Example problem:

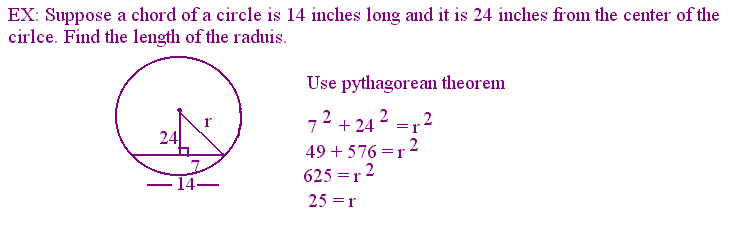
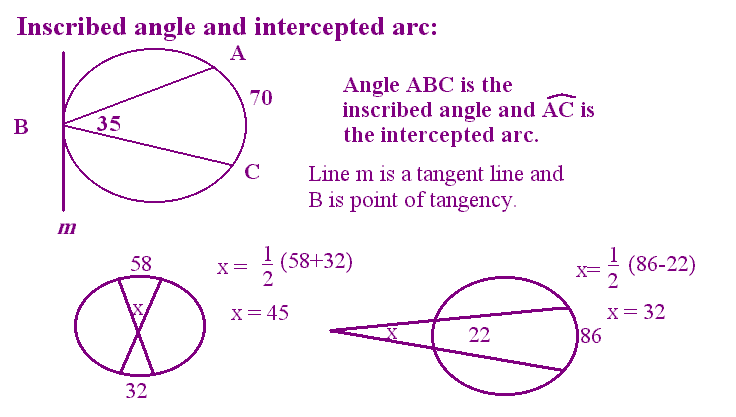
Inscribed angle is an angle in the circle with vertex on the circle.

Intercepted arc is the arc included by the inscribed angle.

*Inscribed angle is half of the intercepted arc.*

Tangent of a circle is a segment the touches the circle in ONE point.

Point of tangency is the point where the tangent touches the circle.

*The tangent line is perpendicular to a radius of the circle.*

Secant is a segment that touches the circle in TWO points.

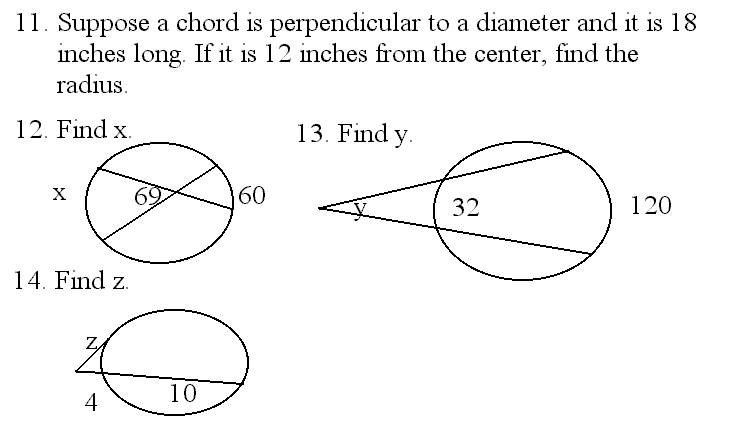
If two secants intersect in the circle, then the angle is half the sum of the intercepted arcs.

If two secants intersect outside of the circle, then the angle is half the difference of the intercepted arcs.

Examples:

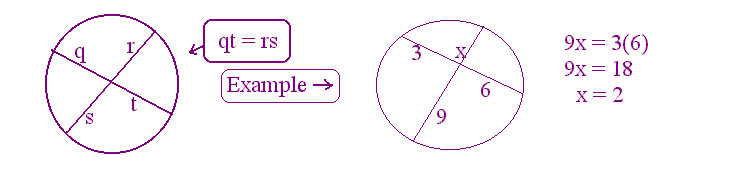
Special segments in a circle:

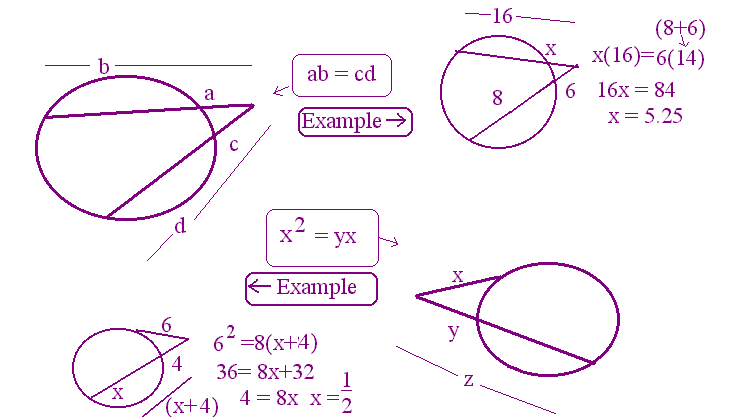
Example Problems